If y=f(x)=x 2/x-1 then show that x=f(y) 255149

Updated October 22, 07 1 Introduction It is well known that exponential functions f(x)=ekx, for any k 2R, are isomorphisms from addition to multiplication, ie for all x;y 2RAnd compare the resulting equation with (1) to conclude that f(y) = f(y), ie / is even If f(G) ç {1, 1} then fix y) = f(xy)=\ if f(x)f(y) = 1 and fix y) = fix y) = 1 if/(x)/(y) = 1 In this case/(x y) = f(x)f(y) for all x, y G G so that (2) and (3) hold with m = f To complete the proof we may assume fia)2 ¥= 1 for some a G GClick here👆to get an answer to your question ️ If F(x) = then show that F(x)F(y) = F(x y) Hence prove that F(x)^1 = F( x)

Multiplicative Inverse Wikipedia

If y=f(x)=x 2/x-1 then show that x=f(y)

If y=f(x)=x 2/x-1 then show that x=f(y)-May 31, 21 · If y = f(x) = `(x2)/(x1) , x ne1` , then show that x = f(y)Notes on discontinuous f(x) satisfying f(xy)= f(x)f(y) Steven G Johnson Created February 15, 07;

If Y F X X 2 X 1 X Ne1 Then Show That X F Y

Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyIf xy=2 and x−y=1, then what is xy?Ch 26 Formulate a precise definition of limxf(x)= Then Ch 26 (a) Prove that limxf(x)=limt0f(1/t) and Ch 27 A curve has equation y = f(x) (a) Write an Ch 27 Graph the curve y = ex in the viewing rectangles Ch 27 (a) Find the slope of the tangent line to the Ch 27 (a) Find the slope of the tangent line to

Divide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side of the equation a perfect squareGraph f (x)=1/2x1 f (x) = 1 2 x − 1 f ( x) = 1 2 x 1 Rewrite the function as an equation y = x 2 −1 y = x 2 1 Rewrite in slopeintercept form Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m xJun 19, 19 · If y=f(x)=x2/x1, x,y is not=1 then x is equal to 1 See answer Snehapareek975 is waiting for your help Add your answer and earn points rahman786khalilu rahman786khalilu Stepbystep explanation hope it helps mark as brainliest New questions in Math Post the answers only of the given questions

Let f be defined for all real x, and suppose that jf (x)¡ f (y)j•(x¡y)2 for all real x and y Prove that f is constant Solution For x 6˘y, from the above inequality we have jf (x)¡f (y)j jx¡yj •jx¡yj So then jf 0(y)j˘ fl fl fl fllim x!y f (x)¡ f (y) x¡y fl fl fl˘ lim x!y fl fl fl f (x)¡ f (y) x¡y fl fl fl• limIf (x, y) belongs to the set defining f, then y is the image of x under f, or the value of f applied to the argument x In the context of numbers in particular, one also says that y is the value of f for the value x of its variable, or, more concisely, that y is the value of f of x, denoted as y = f(x)(b) 2 x y dx ( y 2 x 2) dy = 0 Here, M = 2 x y, M y = 2x, N = y 2 x 2, and N x = 2 xNow, ( N x M y) / M = ( 2 x 2 x ) / ( 2 x y) = 2 / yThus, μ = exp ( ∫ 2 dy / y ) = y2 is an integrating factor The transformed equation is ( 2 x / y ) dx ( 1 x 2 y2) dy = 0 Let m = 2 x / y, and n = 1 x 2 y2Then, m y = 2 x y2 = n x, and the new differential equation is exact

If F X X 1 X 1 Then Prove That F 2x 3f X 1 F X 3 Brainly In

Presentation Exercises 18 1018 Studocu

Dec 08, 12 · For example you can prove using some algebra that if f is defined by f(x)=(ax1)(xd) where a^2=d^2=1 and ad0 then f(f(x))=1/x for all real x Choosing a=1,d=1, this give a solution to the problem in C(a)Show if f 1(x) f 2(x) for all xin some interval (a;b), then L 1 L 2 Hint You may use the results on limits of sequences If x n!L 1 and y n!L, and x n y nfor each n, then L 1 L 2 See Exercises and 99 (b)Suppose that, in fact, f 1(x)If F(x)=x has no real solution then also F(F(x)=x has no real solution

Notes 9 09 Independence Studocu

Gamma Function Intuition Derivation And Examples By Aerin Kim Towards Data Science

This is a very common IBlevel question, which is solved with using the technique of a "disguised quadratic" The first thing we want to do in finding the inverse is swapping the places of x and y in the equation y=f(x), to obtain x=f(y), because finding the inverse is equivalent to reflecting the curve in the line y=x, ie interchanging the x and y coordinatesTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `f (x/y)= f(x)/f(y)` ,`AA y, f (y)!=0` and `f' (1) = 2`, find f(x)Df = f 0(x 0) dx x x 0 L(x) y f(x) x df dx = x f f(x ) 0 Differential of functions of more than one variable Definition The differential at (x 0,y 0) ∈ D of a differentiable function f D ⊂ R2 → R is the linear function df (x,y) = L(x,y) − f (x 0,y 0) Remark The linear approximation of f (x,y) at (x 0,y 0) is the plane L(x,y

9 Hy Log X Vx2 1 Then Cy X 10 S 001sinx Coaxi

Determine Whichofthe Followin See How To Solve It At Qanda

Sep 17, 17 · The answer is =lnx I assumed that f(x)=e^x Let, y=e^x The domain of x is RR The range of y is RR**^ f(x) and f^1(x) are reflections in the line y=x Then ln(y)=ln(e^x) lny=x x=lny Exchanging x and y in the last equation y=lnx So, the inverse is f^1(x)=lnx Verification by performing the composition of the functions fof^1(x)=f(f^1(x))=f(lnx)=e^(lnx)=x graph{(yx)(ye^x)(xe^yBasically, the function has to be "onetoone" and "onto" The absolute value function isn't onetoone, because although every x in the domain maps to only one y in the range, not every y in the range is mapped to by only one x But IF the function is invertible, then f (x)=f (a) will imply x=aApr 08, 13 · The functional equation f (xy) = f (x)f (y) Suppose satisfies What can we say about ?

Graphing Parabolas

If Y F X 1 X 1 X Then Show That X F Y Maths Relations And Functions Meritnation Com

Find the right hand derivative and the lrft hand derivative of f(x)=x1, x2 =2x3, x ≥ 2 at the point x=2 and hence show that f(x) is not differentiable at x=2F (xy)f (x) = f (y) 2xy If we divide both sides by y, and take the limit of both sides, as y approaches 0, we get f' (x)= 2x (limit as y→0) f (y)/y Since f (0) is 0 from the initial conditions (put x=y=0 in the original expression), we have a 0/01 Let y = x 1 x, try now to express x as a function of y We have x 2 − x y 1 = 0 x = y ± y 2 − 4 2 Substitute this value for x in your expression for f f ( y) = ( y ± y 2 − 4 2) 2 ( 2 y ± y 2 − 4) 2 f ( y) = y

Multiplicative Inverse Wikipedia

Consider The Function F X Y Xy X 2 Y 2 X Chegg Com

If X and Y are independent, then f(x, y) = f_x(x)f_y(y) If X and Y are uncorrelated, then E(XY) = E(X)E(Y) The correlation coefficient between X and Y is rho_xy = sigma_xy/(sigma_x sigma_y) Eg(X, Y) = integral_S_r integral_S_x g(x, y) f_(x, y)(x, y) dxdy For any function g(x, y), Cov(aX bY c, W) = a sigma_xy b sigma_yw Var(aX bY C) = a^2 sigma_x^2 b^2 sigma_y^2 Var(aXApr 25, 18 · f^(1)(x)=sqrt(x1) Let y=f(x) Then, y=x^21 To determine the inverse function, switch the places of x and y, and subsequently solve for y x=y^21 y^2=x1 y=sqrt(x1) Since this is the inverse, y=f^(1)(x) f^(1)(x)=sqrt(x1)Chapter 11 which is the equation of a plane 112 Implicit Functions The totality of points (x,y) satisfying the equation F(x,y) = 0 forms a curveGiven a value of the independent variable x, evaluation of y, supposing one exists, may require the approximate solution of F(x,y) = 0 by numerical means, such as the method of bisections or the metod of successive linearizations

Prove That If F Is Continuous On Some Subset E K Chegg Com

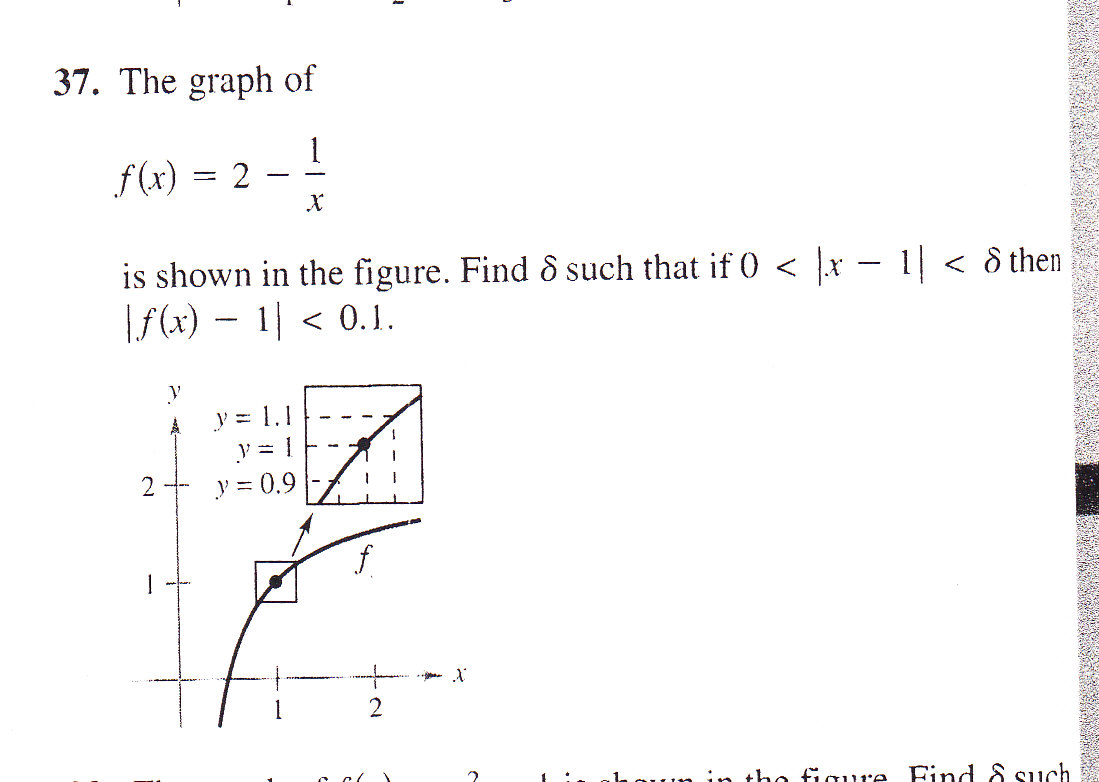
Solved The Graph Of F X 2 1 X Is Shown In The Figure Chegg Com

Calculus Multivariable Calculus Homogeneous Function Show that if f ( x, y ) is homogeneous of degree n, then x f x ( x , y ) y f y ( x , y ) = n f ( x , y ) Hint Let g ( t ) = f ( t x , t y ) = t n f ( x , y ) Find g' ( t ) and then let t = 1Aug 22, 17 · Given, y = f(x) = (x 2) / (x 1) where ,(x ≠1,2) Now, f(y) = (y 2) / (y 1) = { (x 2) / (x 1) } 2 } / { (x 2) / (x 1) } 1 = 3x / 3 = x Hence, f(y) = x hence proved =====Jul 23, 15 · Share 1 Follow 0 Anuradha Sharma, Meritnation Expert added an answer, on 23/7/15 Anuradha Sharma answered this f x = x x 1 = 1 y y = x 1 x xy = x 1 x y 1 = 1 x = 1 1 y So f y = 1 y = 1 x This conversation is already closed by Expert

Chapter 5 Limits And Continuity Ppt Download

If F X X 1 X 1 Then Show That F 2x 3f X 1 F X 3 Maths Relations And Functions Meritnation Com

Jan 28,  · Ex 13, 6 Show that f −1, 1 → R, given by f(x) = 𝑥/(𝑥 2) is oneone Find the inverse of the function f −1, 1 → Range f (Hint For y ∈ RangeExample OLS in parallel universes In each simulation, given the design matrix X and Y, we build a tted model f^using ordinary least squares Finally, let XHowever there can exist

Even And Odd Functions Equations Video Khan Academy

4 Ways To Find The Range Of A Function Wikihow

Example 1 f(x) = x We'll find the derivative of the function f(x) = x1 To do this we will use the formula f (x) = lim f(x 0 0) Δx→0 Δx Graphically, we will be finding the slope of the tangent line at at an arbitrary point (x 0, 1 x 1 0) on the graph of y = x (The graph of y = x 1 is a hyperbola in the same way that the graph of yX y = 2 (equation 1) x y = 1 (equation 2) Add the equations for 2x = 3, meaning that x = 3/2 Using x = 3/2 in equation 1 gives y = 1/2 Using x = 3/2 in equation 2 also gives y = 1/2 (3/2)*(1/2) = 3/4 AnswerGraph f (x)=2 f (x) = 2 f ( x) = 2 Rewrite the function as an equation y = 2 y = 2 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the

Math 317 Hw 9 Solutions

Function Mathematics Wikipedia

Solution u = sin 1 ( (x 2 y 2 )/ (xy)) sin u = (x 2 y 2 )/ (xy)) = x 2 (1y 2 /x 2 )/x (1y/x) = x (1y 2 /x 2 )/ (1y/x) = x f (y/x) This is a homogeneous function of degree 1 So by Euler's theorem x∂z/∂x y ∂z/∂y = nzSteps for Solving Linear Equation f ( x ) = 1 \frac { 2 } { x 1 } , s f ( x) = 1 − x 1 2 , s Multiply both sides of the equation by x1 Multiply both sides of the equation by x 1 fx\left (x1\right)=x12 f x ( x 1) = x 1 − 2 Use the distributive property to multiply fx by x1For the usual y = f(x), the input is x and the output is y For the INVERSE function x = f^1(y), the input is y and the output is x If y equals x cubed, then x is the cube root of y that is the inverse If y is the great function e^x, then x is the NATURAL LOGARITHM ln y Start at y, go to x = ln y, then back to y = e^(ln y)

Math Problems With Solutions Pdf Free Download

Solved Question 6 3 Marks Let A Be A Positive Real Numb Chegg Com

GENERAL ARTICLE Since f is an odd function, it follows that f(x) =cxfor all x ∈Q f(0) =2f(0) and hence f(0) =0Let c =f(1) and by appealing to (01) once again, note that f(2) =f(1)f(1) =2c By induction, it follows that f(n) =cn for every integer n ≥1 But then 0 =f(0) =f(x(−x)) =f(x)f(−x), for every x ∈R and this shows that f(x) =−f(−x), ie, f is an odd functionMATH 140B HW 1 SOLUTIONS Problem1(WR Ch 5 #6) Suppose (a) f is continuous for x ‚0, (b) f 0(x) exists for x ¨0, (c) f (0) ˘0, (d) f 0 is monotonically increasing, Put g(x) ˘ f (x) x (x ¨0)and prove that g is monotonically increasing Solution If we can prove that g0(x) ¨0 for x ¨0, then this will show that g is monotonically increasing (by Theorem 511a) By the quotient rule,Cauchy's functional equation is the functional equation () = () Solutions to this are called additive functionsOver the rational numbers, it can be shown using elementary algebra that there is a single family of solutions, namely ↦ for any rational constant Over the real numbers, ↦, now with an arbitrary real constant, is likewise a family of solutions;

Example 11 Show F X X2 Is Neither One One Nor Onto Examples

If Y F X X 2 X 1 X Ne1 Then Show That X F Y

Jan 17,  · Ex 32, 13 If F (x) = 8(cos⁡𝑥&〖−sin〗⁡𝑥&0@sin⁡𝑥&cos⁡𝑥&0@0&0&1) , Show that F(x) F(y) = F(x y) We need to show F(x) F(y) = F(x y) Taking LHS Given F(x) = 8(cos⁡𝑥&〖−sin〗⁡𝑥&0@sin⁡𝑥&cos⁡𝑥&0@0&0&1) Finding F(y) Replacing x by y in F(x) F(y) = 8(cos⁡𝑦&〖−sin〗⁡𝑦&0@sin⁡𝑦&coJun 15, 13 · given, f(x) = x1/x1 we can also write f(y) = y1/y1 let y= f{(x)} ff{(x)} = f{(x)} 1/ f{(x)} 1 solving lhs ff(x) = fx1/x1 putting value in rhs (x1Just replace x with n1 to obtain so choice C is correct

Example 11 Show F X X2 Is Neither One One Nor Onto Examples

Functional Equations Pdf Free Download

If 0 x0 since each of the two factors is >0 Thus, f(x)Solution for f (xy)f (xy)=2F (x)F (y) equation Simplifying f (x y) f (x 1y) = 2F (x) * F (y) (x * f y * f) f (x 1y) = 2F (x) * F (y) (fx fy) f (x 1y) = 2F (x) * F (y) fx fy (x * f 1y * f) = 2F (x) * F (y) fx fy (fx 1fy) = 2F (x) * F (y) Reorder the terms fx fx fy 1fy = 2F (x) * F (y) Combine like terms fx fx = 2fx 2fx fy 1fy = 2F (x) * F (y) Combine like terms fy 1fy = 0 2fx 0 = 2F (x) * F (y) 2fx = 2F (x) * F (y) Multiply F * xQuestion If f (x)= x2/x1, then f (n1) is equal to A)1/2 b)n2/n1 c)n1/n2 d)n1/n2 Answer by richard1234 (7193) ( Show Source ) You can put this solution on YOUR website!

Suppose F X Is Continuous X In 0 Infty F 0 0 If For Any Positive X And Y It Holds That F X Y F X F Y Can You Prove That F X Is Concave

The Third Calculus Competition Of Uw La Crosse

Which can happen if either or Note that the function which is identically zero satisfies the functional equation If is not this function, ie, if for at least one value of , then plugging that value of (say ) into the equation givesSep 11,  · Let f(x, y) be a periodic function which satisfies the condition f(x, y) = f(2x 2y, 2y 2x) ∀x, y ∈ R asked Dec 2, 19 in Sets, relations and functions by RiteshBharti ( 538k points) sets

6 Ways To Find The Domain Of A Function Wikihow

Finding Derivative With Fundamental Theorem Of Calculus Video Khan Academy

212 Questions With Answers In Functional Analysis Science Topic

Reflect Function About Y Axis F X Expii

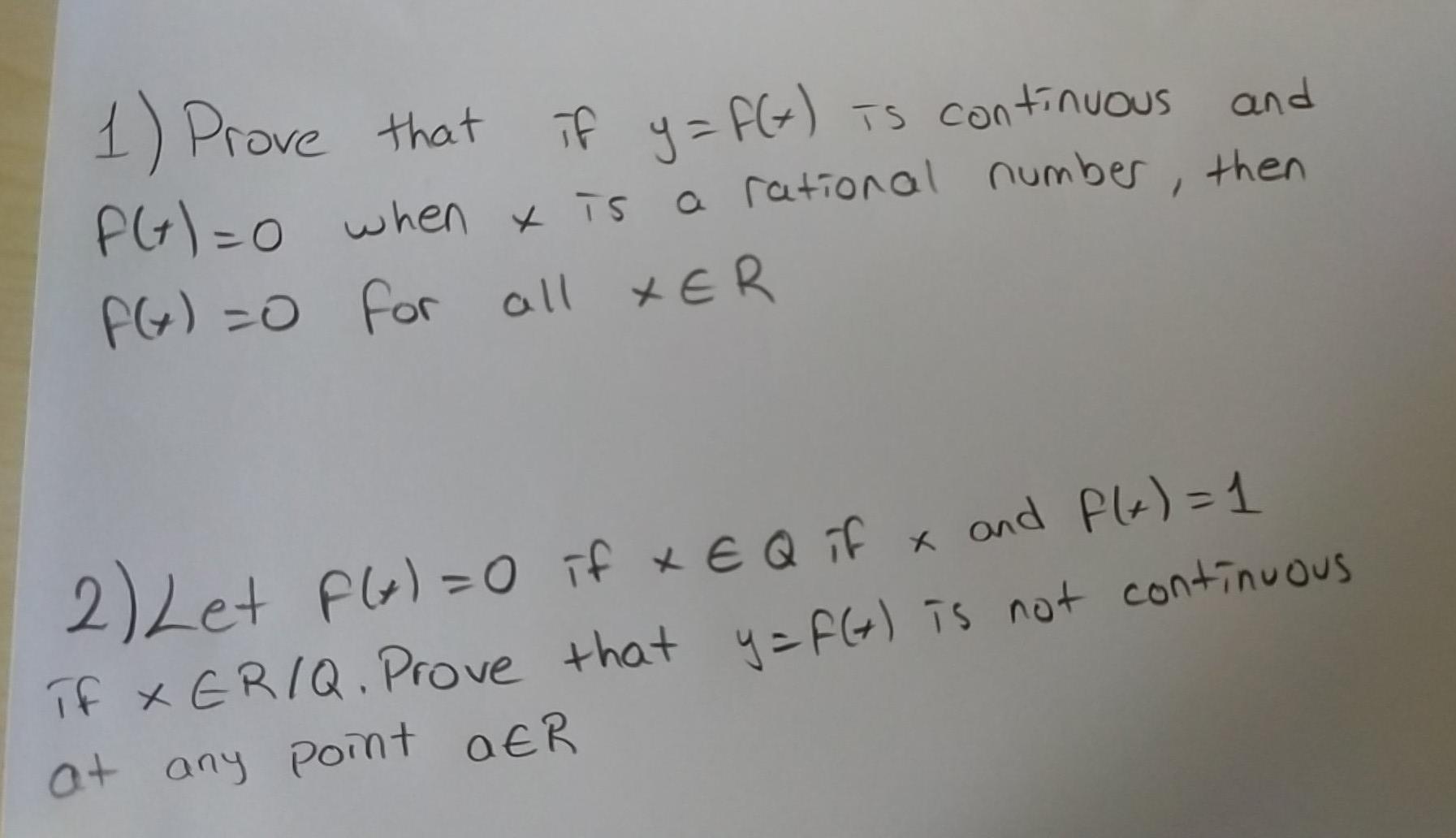
Solved If Xeriq Prove That Y F Is Not Continuous If Y Chegg Com

Derivatives Of Inverse Functions Video Khan Academy

Solved A Function F Is One To One Or Injective If And Onl Chegg Com

1 If F X 5 For All Values Of X Then Delta F X

Horizontal Line Test For Function To Have Inverse Expii

Derivatives Of Inverse Functions From Equation Video Khan Academy

Ax B And G X Cx

Finding Composite Functions Video Khan Academy

Olympiad Corner Functional Inequalities Math Ust Hk Volume 21 Number 3 October 17 January Pdf Document

Exactly five R A B But Not Uniformly Flip Ebook Pages 1 5 Anyflip Anyflip

Rd Sharma Class 9 Solutions Maths Chapter 6 Factorization Of Polynomials

Solved F Left X Right Frac 1 X 1 1 Left 1 1 3 Righ Chegg Com

Example 16 Let F X X2 And G X 2x 1 Find F G Fg F G

Answered Dtant X V X Xy 4 Xv Al 4 2xytx 4 Bartleby

Using Transformations To Graph Functions

Tutorial Sheet 5 Assignment Studocu

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

Example 16 Let F X X2 And G X 2x 1 Find F G Fg F G

Finding The Inverse Of A Function Youtube

If Y F X X 2 X 1 X Y 1 Then X Is Equal To

Let F X Ln 1 X 1 X Find X Y For Which F X F Y F X Y

If F X Tex Frac X 1 X 1 Tex X 1 Then Verify Fof X X Brainly In

1 If 1 X 0 1 If 0 X 1 Pdf Free Download

Lots Of Questions Pdf Prime Number Numbers

If F Y Logy Then F Y F 1 Y Is Equal To

Partial F X Y X F X X2 Y2 And Then We Evaluate The Derivative As If Y Is A Constant Pdf Free Download

If F X 1x 2 4x 4 4x 4 4x 2 4x 2 4x 3 2x 2 Then F 12 Is Equal To

Assignment 2 Continuity Differentiability Derivative Sine

How To Compute The Difference Quotient F X H F X H Youtube

Answered D Y 0 140 If Y X 1 X 2 X Bartleby

Ex 1 2 10 F X X 2 X 3 Is F One One Onto Class 12